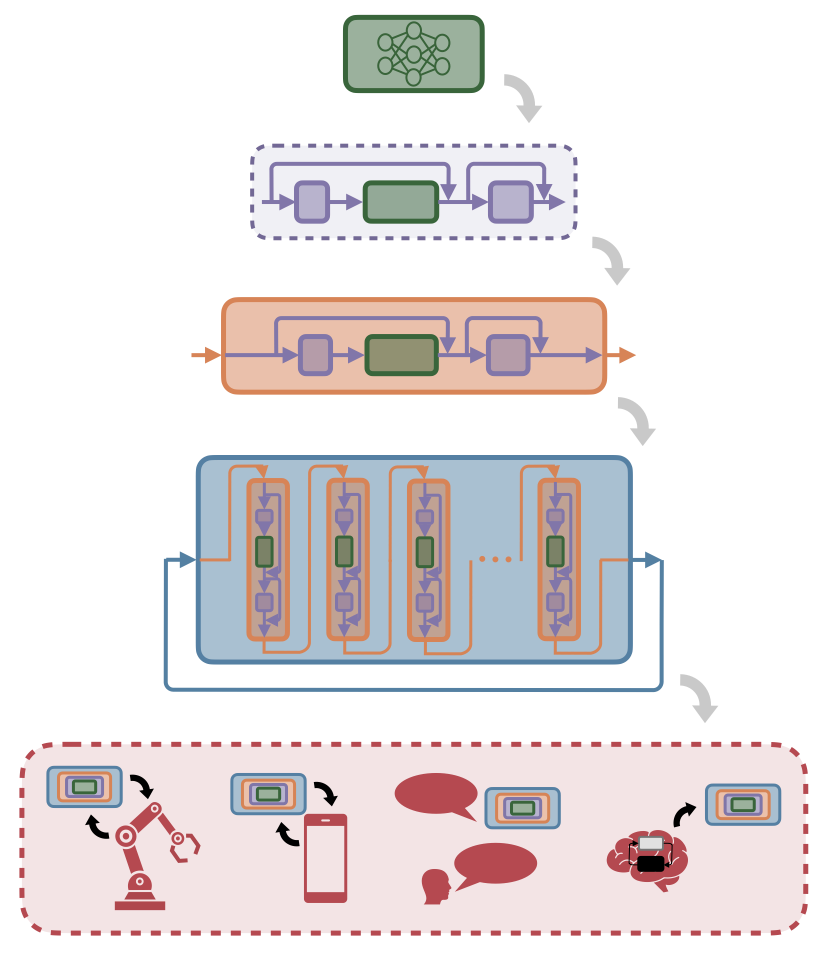
Mixer Block: The mixer block sits at the core of an AI architecture and is responsible for mixing sequence tokens. Attention, the recurrent block in SSMs, etc.; are mixer blocks. By studying how these tokens evolve and interact over time, we can better compare different popular architectures (paper). This perspective also helps build a foundation for more principled design ideas in a field that's still mostly guided by empirical benchmarks (paper).

Surrounding Components: The surround components scaffold the mixer block to pre- and post-process the signal. By studying these components, we can gain important insights about their dynamics. For instance, a dynamical systems perspective sheds light on how skip connections contribute to the rank collapse phenomenon (paper), and clarifies the influence of layer normalization on optimization dynamics (coming soon!).

Single Layer: Together, a mixer block and its surrounding components make up a layer. We can study the layer as an input-output dynamical system, agnostic to its internal dynamics. The dynamics emerge when viewing stacked layers as different points in time of a single dynamical system. In this way, steering activations during generation becomes a control problem (paper). This line of work provides a foundation for controlled generation with theoretical guarantees.

Deep AI Architecture: We can also study a Transformer as a dynamical system. This way, we have a principled analysis of the global behavior of the AI generative model. For autoregressive models, this viewpoint allows the study of the closed-loop dynamics that emerge during generation. We can use classical tools such as reachability and controllability to answer questions such as whether internal states can be inferred from outputs, whether desired outputs can be reached given an input, and how the model explores the latent space during generation (coming soon!).

AI Systems: Lastly, AI generative models are embodied in cyber or physical systems. These, are themselves dynamical systems. For instance, we can study how to interface Language Models with controllers using the geometry of the embedding space for robot control (paper, paper). We can also study how AI recommender systems control the opinion dynamics of a population (coming soon!). Or can use our control generation strategies for multi-lingual translation in natural language processing (coming soon!). All of this, while taking inspiration from neuroscience and how natural intelligent systems are implemented (paper).

Studying AI systems with the lenses of dynamical systems holds great promise to achieve (a) principled design strategies, and (b) controllable architectures with guarantees. These aspects, present in most engineering developments, are currently lacking in AI. I argue, that developing principled and controllable AI is important for two reasons: (a) The current ad-hoc trial-and-error design of AI systems is highly compute and energy intensive: a principled approach to AI design would accelerate its development in a more resource-efficient manner. (b) Current AI systems require enormous amounts of data, computation, and engineering oversight to achieve a basic level of safety: developing controllable AI systems will enable the use of AI in critical infrastructure without excessive overhead. And while the use of control theory in AI systems is promising, the traditional control theory that has enabled principled and controllable designs in other engineering systems does not directly port to AI. The reason is that AI systems exhibit extraordinary complexity through massive scale, sparse topologies, and local communications. Fortunately, my research on the foundations of distributed optimal control for large-scale systems addresses these issues!

Distributed Optimal Control for Large-Scale Systems

The internet, the power network, a fleet of autonomous cars, or bacterial metabolism: large-scale networks are everywhere! We would like to design strategies to control their behavior in the same way that we do for centralized systems (a single car, an aircraft, etc.). However, these networks are composed by many agents (subsystems) that can only communicate to a few neighbors. The sparsity of the networks has been seen as a major challenge, as they hinder the global communication exchanges. This sparsity creates significant computational and communication bottlenecks that traditional centralized control approaches cannot handle efficiently. Distributed control strategies must therefore be designed to work within these communication constraints while still achieving optimal or near-optimal performance across the entire network.

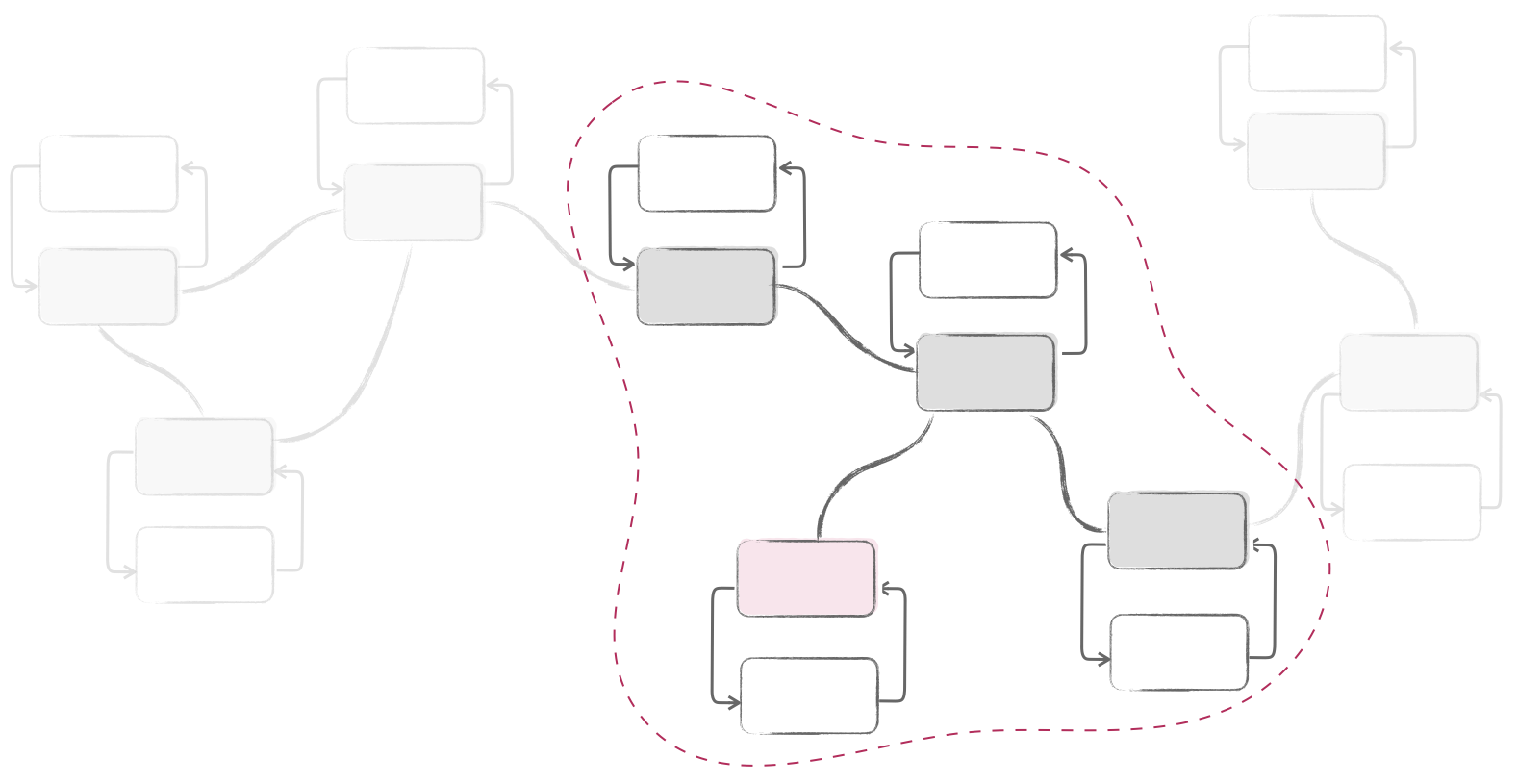
Contrary to prior works, my Ph.D. research capitalizes on this sparsity: we restrict each agent in the network to only communicate with a small neighborhood of agents as opposed to the entire network. By integrating ideas from control theory, optimization and learning into this framing, we developed a new set of algorithms and theoretical results to optimally control distributed bio and cyber-physical systems for safety-critical applications: the Distributed and Localized Model Predictive Control (DLMPC) framework! In this framework, both the controller synthesis and implementation are fully distributed and scalable to arbitrary network sizes (see details here). Also, we provide theoretical guarantees for asymptotic stability and recursive feasibility without strong assumptions, ensuring minimal conservativeness, no added computational burden, and scalable computations (see details here). Furthermore, our framework is applicable even when no model of the system is available and only past trajectories can be used. In this scenario, each agent only needs to gather data from its local neighborhood, making the approach suitable for large-scale networks (see details here).

Our findings indicate that restricting communication to a small neighborhood can yield significant computational benefits. This leads us to an important question: what are the trade-offs? Are the resulting policies less optimal than those that allow communication across the entire network? We demonstrate that for sparse systems, including local communication constraints can be as optimal as centralized MPC while enhancing scalability (see details here). This result paves the way for broader applications of DLMPC. Besides distributed systems, DLMPC can replace the standard MPC in centralized systems to accelerate computations. Given that current GPUs also operate with local communication exchanges, DLMPC computation can be naturally parallelized in GPU (see details here).

Together, these different frontiers can be layered to create effective and scalable control architectures for real-world large-scale systems. My PhD work shows how all this can be achieved by leveraging the intrinsic and ubiquitous sparsity of large-scale distributed systems in technology and biology.